Question

An Tower is 70 m high. A support wire is attached to the tower 20 m from the top. If the support wire and the ground form an angle of 46°, what is the length of the support wire, to the nearest 10th.

Answer 1

The tower is 70 m high and and the wire is knoteed from the top of 20 m of the tower,

Here, AB represent the tower, AB = 70m

and AD represent the 20 m from the top, AD = 20m

SInce the wire is knotted from the top of 20m i.e. the wire is knotted at point D

Thus, BD = AB - AD

BD = 70 - 20

BD = 50m

The wire is knotted to the ground at point C;

and Angle C = 46°

Here, we need to find the length of the wire, i,e we need to find the length of side CD

In the diagram, CBD makes a right angle triangle,

Angle C = 46, and the side opposite to the angle C is BD = 50 and Hypotenuse CD

Apply the trigonometric ratio of Sine of angle 46

Since,

`\sin \theta=\frac{Opposite\text{ side}}{Hypotenuse}`

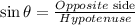
Substitute angle = 46, Opposite side BD = 50 and Hypotenuse CD

`\begin{gathered} \sin \theta=\frac{Opposite\text{ side}}{Hypotenuse} \\ \sin 46=(BD)/(CD) \\ CD=(BD)/(\sin 46) \\ CD=(50)/(0.719) \\ CD=69.54\text{ m} \end{gathered}`

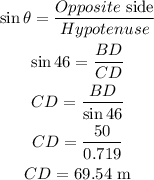
Therefore, the length of the wire is 69.54 m

Answer: 69.5m