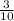Question

What is the probability of flipping heads on a coin and then spinning a number greater than 6 on a spinner that is divided into 15 equal sectors numbered 1 through 15? Enter your answer, as a simplified fraction, in the boxes.

Answer 1

P(H) = 1/2
P(>6) = 9/15 = 3/5

P(Both H AND >6) = 1/2 * 3/5 = 3/10

Answer 2

The probability of flipping heads on a coin and then spinning a number greater than 6 on a spinner is
`(3)/(10)`

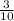
Explanation:

To find : What is the probability of flipping heads on a coin and then spinning a number greater than 6 on a spinner that is divided into 15 equal sectors numbered 1 through 15?

Solution :

In flipping a coin outcomes are {H,T} = 2

Favorable outcome of getting head on a coin {H}=1

The probability of flipping heads on a coin is

`P(H)=(1)/(2)`

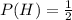
Spinner that is divided into 15 equal sectors numbered 1 through 15.

Favorable outcome of getting a number greater than 6 {7,8,9,10,11,12,13,14,15}=9

The probability of spinning a number greater than 6 is

`P(S)=(9)/(15)`

`P(S)=(3)/(5)`

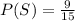
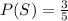
Now, The probability of flipping heads on a coin and then spinning a number greater than 6 on a spinner is given by,

`P(H\text{ and } S)=P(H)* P(S)`

`P(H\text{ and }S)=(1)/(2)*(3)/(5)`

`P(H\text{ and }S)=(3)/(10)`

Therefore, The probability of flipping heads on a coin and then spinning a number greater than 6 on a spinner is
`(3)/(10)`