Answer:
The kinetic energy of the larger car is two times that of the smaller car
Step-by-step explanation:
Kinetic Energy
Is the energy an object has due to its state of motion. It's proportional to the square of the speed.
The equation for the kinetic energy is:
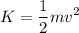
Where:
m = mass of the object
v = speed at which the object moves
The kinetic energy is expressed in Joules (J)
It's required to compare the kinetic energy of two cars K1 and K2. Car 2 has twice the mass of car 1: m2=2m1, and they have the same speed.
The kinetic energy of car 1 is:
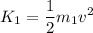
The kinetic energy of car 2 is:

Substituting the relation of the masses:

Rearranging:
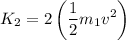
Substituting the kinetic energy of car 1:

The kinetic energy of the larger car is two times that of the smaller car