Question

My answer is unique triangle but I'm not sure if my answer is right

Answer 1

In any triangle, the following inequalities must be fulfilled:

Question 1.

1A. In this case, we get

`\begin{gathered} 12+5>17\Rightarrow17>17\text{ Thats incorrect.} \\ 5+17>12\Rightarrow22>12\text{ Thats correct.} \\ 12+17>5\Rightarrow29>5\text{ }12+5>7\Rightarrow17>7\text{ Thats correct.} \end{gathered}`

Then, these side cant make a triangle.

1B. In this case, we have

`\begin{gathered} 10+15>24\Rightarrow25>24\text{ thats correct !} \\ 15+24>10\Rightarrow39>10\text{ thats correct !} \\ 10+24>15\Rightarrow34>15\text{ thats correct !} \end{gathered}`

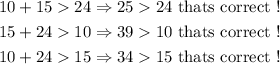
Then, these side can make a triangle.

1C. In this case, we obtain

`\begin{gathered} 9+22>11\Rightarrow31>\text{ thats correct} \\ 22+11>9\Rightarrow33>9\text{ thats correct} \\ 9+11>22\Rightarrow20>22\text{ thats incorrect !!} \end{gathered}`

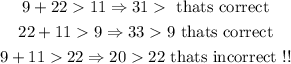
then, thesesides cant make a triangle.

1D. In this case,we have

`\begin{gathered} 21+7>6\Rightarrow28>6\text{ thats correct} \\ 7+6>21\Rightarrow13>21\text{ thats incorrect !!} \end{gathered}`

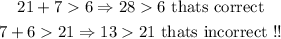
then, thesesides cant make a triangle.

Now, lets continue with question 2.

2a) In this case, we get

`\begin{gathered} 23+17>14\Rightarrow40>14\text{ thats correct} \\ 17+14>23\Rightarrow31>23\text{ thats correct} \\ 23+14>17\Rightarrow37>17\text{ thats correct} \end{gathered}`

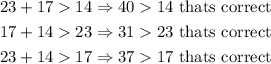
then, these sides can make a triangle

2b) In this case, we have

`\begin{gathered} 11+11>12\Rightarrow22>12\text{ thats correct} \\ 11+12>11\Rightarrow23>11\text{ thats correct} \\ 11+12>11\Rightarrow23>11\text{ thats correct} \end{gathered}`

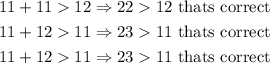
then, these sides can make a triangle

2c) In this case, we have

`\begin{gathered} 5+7>8\Rightarrow12>8\text{ thats correct} \\ 7+8>5\Rightarrow15>5\text{ thats correct} \\ 5+8>7\Rightarrow13>7\text{ thats correct} \end{gathered}`

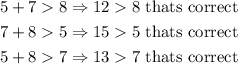
then, these sides can make a triangle.

2d. Finally, in this case we get

`\begin{gathered} 21+6>10\Rightarrow27>10\text{ thats correct} \\ 6+10>21\Rightarrow16>21\text{ thats incorrect !!} \end{gathered}`

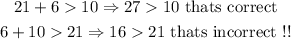
then, these sides can't make a triangle.

Now, lets continue with question 3. We know that interior angles of any triangle add up to 180 degrees. So, we have

3a) 47+58+75=180, then, these angles can make a triangle.

3b) 61+61+58=180, then, these angles can make a triangle.

3c) This case is similar to question 1 and 2, that is

`\begin{gathered} 5.5+11>5.5\Rightarrow16.5>5.5\text{ thats correct} \\ 11+5.5>5.5\Rightarrow16.5>5.5\text{ thats correct} \\ 5.5+5.5>11\Rightarrow11>11\text{ thats incorrect !!!} \end{gathered}`

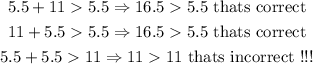
then, these sides can't make a triangle.

3d) In this case, we have

`\begin{gathered} 5+7>8\text{ thats correct} \\ 7+8>5\text{ thats correct} \\ 5+8>7\text{ thats correct} \end{gathered}`

then, these sides can make a triangle.

Question 4. The above inequalities can be written in a more succinct form:

[tex]|a-b|where the bars denote the absolute value. In our case, we have[tex]|5-9|which gives[tex]|-4|but absolute value of -4 is 4, then the answer is option D:[tex]4