Answer:

Explanation:
The general exponential function is given by :-
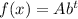 , where A is the initial amount , b is the multiplicative rate of change and t is the time period.
, where A is the initial amount , b is the multiplicative rate of change and t is the time period.
From , the given table the value of the function at t=0 is 180.
i.e the initial amount of radioactive material = 180
Also, the multiplicative rate is the common ratio of the values of the function w.r.t. to time
The multiplicative rate =
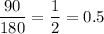
Now, the exponential function best represents the relationship between f(t) and t will be :-
