Given:
• Height of image = 8.00 cm
,
• Distance from convex = 46.5 cm
,
• Focal length = 16.0 cm
Let's find the image distance.
To find the image distance, apply the formula below.
Equation:
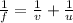
Required:
f = 16.0 cm
u = 46.5 cm
Let's solve for v
We have:
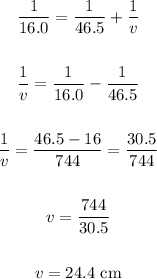
Now apply the formula to find the height:
![\begin{gathered} h^(\prime)=(-v* h)/(u) \\ \\ h^(\prime)=(-24.4*8.00)/(46.5) \\ \\ h^(\prime)=-4.2\operatorname{cm} \end{gathered}]()
Therefore, the distance is 24.4 cm
The height of the object is -4.2 cm
ANSWER:
Given: f = 16.0 cm; u = 46.5 cm, h = 8.00 cm
Required: v and h'
Equations needed:
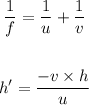
Solution: v = 24.4 cm
h' = -4.2 cm
L-ocation: Behind the mirror
O-rientation: Inverted
S-ize: Reduced
T-ype: Real