Question

triangle RST is congruent to triangle NPQ, RT=7x-5, NQ= 5x+11, find the length of side RT and side NQ

Answer 1

7x + 5 = 5x + 11
2x + 5 = 11
2x = 6
x = 3

7(3) + 5
21 + 5 = 26

Answer 2

Answer: The length of side RT and side NQ is 51 units.

Explanation:

Given : Δ RST ≅ Δ NPT

RT=7x-5 , NQ= 5x+11

To find: RT =? and NQ=?

Solution:

Since, given triangles are congruent .And Congruent triangles have equal sides.

`\Delta RST` ≅
`\Delta NPQ`

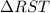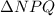
So,

RT= NQ = 7x-5 = 5x+11

Solving for x we get ,x = 8

RT =7x-5 = 7 × (8) - 5 = 51 units

NQ = 5x+11 = 5 × (8) + 11 = 51 units