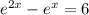
Question

Solve for e^2x-e^x=6

Answer 1

`e ^(2x) -e ^x=6` ----(i)

Let,
`e ^x =t`
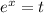
Therefore,
`e^(2x) = t^(2)`

Therefore, from (i),

t²-t=6
t²-3t+2t-6=0
t(t-3)+2(t-3)=0

Therefore, (t-3)(t+2)=0
Therefore, t=3 or t = -2

But,

`e^x =t`

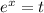
Therefore,


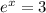
`e^x = 3` or
`e^x = -2`

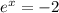
Taking ln on both sides,
Therefore,

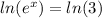
`ln(e^x)=ln(3)` or
`ln(e^x) = ln(-2)`

But natural log of negative numbers does not exist since negative numbers are not in the domain of ln(x)
Therefore,

`ln(e^x) = ln(-2)` is discarded
Therefore, x = ln(3) is the only solution.