Question

Look at these systems of equations. Tell whether the system will have No Solution, OneSolution, or Infinite Solutions. Explainy=2x-10y+3x=5 and 2x+y=26x +3y=6

Answer 1

Answers:

1. One solution

2. Infinite solutions

Step-by-step explanation:

For the first system of equations, we have:

y = 2x - 10

y + 3x = 5

So, we can use the first equation and replace y by (2x-10) on the second equation and solve for x, so:

y + 3x = 5

2x - 10 + 3x = 5

5x - 10 = 5

5x - 10 + 10 = 5 + 10

5x = 15

5x/5 = 15/5

x = 3

Then, we can replace x by 3 on the first equation and calculate y, so:

y = 2x - 10

y = 2(3) - 10

y = 6 - 10

y = -4

Therefore, the first system has one solution and the solution is (3, -4)

On the other hand, for the second system, we have:

2x + y = 2

6x + 3y = 6

So, we can divide both sides of the second equation by 3 and get an equivalent equation as:

`\begin{gathered} (6x)/(3)+(3y)/(3)=(6)/(3) \\ 2x+y=2 \end{gathered}`

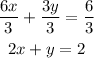
Since the second and first equations are equivalent, the system has infinite solutions.