Question

A certain cylindrical tank holds 20,000 gallons of water which can be drained from the bottom of the tank in 20 minutes the volume tea of water remaining in the tank after T minutes is given by the function (v)= 20,000(1-(t/20)^2 where B is in gallons zero is less than or equal to T which less than or equal to 20 is in a minutes and T equals zero represent the instant the tank starts draining how fast is the water draining 4 1/2 minutes after it begins

Answer 1

Given that the volume of water remaining in the tank after t minutes is given by the function


`V(t)=20,000\left(1- (t)/(20) \right)^2`

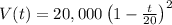
where V is in gallons, 0 ≤ t ≤ 20 is in minutes, and t = 0 represents the instant the tank starts draining.

The rate at which water is draining four and a half minutes after it begins is given by


`\left. (dV)/(dt) \right|_{t=4 (1)/(2) = (9)/(2) }=\left[40,000\left(1- (t)/(20) \right)\left(- (1)/(20) \right)\right]_{t= (9)/(2) } \\ \\ =\left[-2,000\left(1- (t)/(20) \right)\right]_{t= (9)/(2) }=-2,000\left(1- (4.5)/(20) \right) \\ \\ =-2,000(1-0.225)=-2,000(0.775)=-1,550\, gallons\ per\ minute`

Therefore, the water is draining at a rate of 1,550 gallons per minute four ans a half minutes after it begins.

Answer option E is the correct answer.