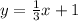The original line we are given is:
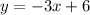
This line is in the slope-intercept form:

where m represents the slope, and b represents the y-intercept of the line.
Step 1. Identify the slope of the original line.
By comparing the given line with the slope-intercept form, we see that the slope m is:
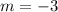
We will rename this slope as m1 because it is the slope of the first line:
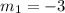
Step 2. The second step will be to find the slope of the second line (the perpendicular line). We will call the slope of the second line m2:
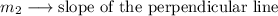
And we will need to apply the condition for the slopes of two perpendicular lines:
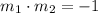
Since what we need to find is m2, we solve for it in the previous equation:
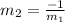
By substituting m1=-2, we can find the slope of the perpendicular line:

The result of this division is:
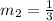
Step 3. Once we know the slope of the perpendicular line, we are ready to find the equation that represents it. Remember that we also have a point through which the line passes:
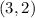
For reference, we will label the x and y coordinates of this point as follows:
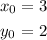
Now, to find the equation of the line we use the point-slope equation:

Where x0,y0 represent the point, and m is the slope, in this case, the slope of the perpendicular line:

We substitute m2, x0, and y0:

And simplify the result in order to solve for y:
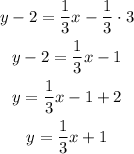
And we have found the equation that represents the perpendicular line.
Answer: