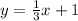Question

Which of the following equations represents a line that is perpendicular toy=-3x+6 and passes through the point, (3, 2)?A. y=-3x+1B. y = x+1O C. y-1x+3O D. y --*x+1SUBMIT

Answer 1

The original line we are given is:

`y=-3x+6`

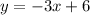
This line is in the slope-intercept form:

`y=mx+b`

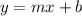
where m represents the slope, and b represents the y-intercept of the line.

Step 1. Identify the slope of the original line.

By comparing the given line with the slope-intercept form, we see that the slope m is:

`m=-3`

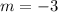
We will rename this slope as m1 because it is the slope of the first line:

`m_1=-3`

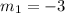
Step 2. The second step will be to find the slope of the second line (the perpendicular line). We will call the slope of the second line m2:

`m_2\longrightarrow\text{slope of the perpendicular line}`

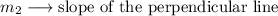
And we will need to apply the condition for the slopes of two perpendicular lines:

`m_1\cdot m_2=-1`

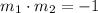
Since what we need to find is m2, we solve for it in the previous equation:

`m_2=(-1)/(m_1)`

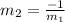
By substituting m1=-2, we can find the slope of the perpendicular line:

`m_2=(-1)/(-3)`

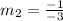
The result of this division is:

`m_2=(1)/(3)`

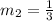
Step 3. Once we know the slope of the perpendicular line, we are ready to find the equation that represents it. Remember that we also have a point through which the line passes:

`(3,2)`

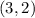
For reference, we will label the x and y coordinates of this point as follows:

`\begin{gathered} x_0=3 \\ y_0_{}=2 \end{gathered}`

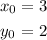
Now, to find the equation of the line we use the point-slope equation:

`y-y_0=m(x-x_0)`

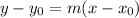
Where x0,y0 represent the point, and m is the slope, in this case, the slope of the perpendicular line:

`y-y_0=m_2(x-x_0)`

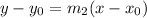
We substitute m2, x0, and y0:

`y-2=(1)/(3)(x-3)`

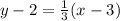
And simplify the result in order to solve for y:

`\begin{gathered} y-2=(1)/(3)x-(1)/(3)\cdot3 \\ y-2=(1)/(3)x-1 \\ y=(1)/(3)x-1+2 \\ y=(1)/(3)x+1 \end{gathered}`

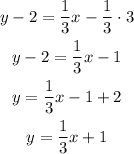
And we have found the equation that represents the perpendicular line.

Answer:

`y=(1)/(3)x+1`