Answer:
Option 2 -
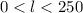
Explanation:
Given : The area of a rectangle with a perimeter of 500 cm is modeled by the function
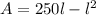 where l is the length of the rectangle.
where l is the length of the rectangle.
To find : Which is a reasonable domain for the context of this situation?
Solution :
A function modeled area of the rectangle is
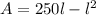
Where, l is the length of the rectangle.
Domain is the complete set of possible values of independent variable.
We know that Area cannot be negative.
So, Put area equals to zero.
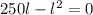

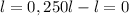
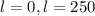
Which means the value of l lies between 0 and 250.
So, The domain of the situation is
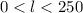 .
.
Therefore, Option 2 is correct.