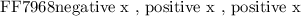Question

Sally plots (-4,pi )on the polar plane.How does she proceed?Drag a phrase to each box to correctly complete the statements.Sally first determineswhich line the angle of rotation places the point on. This line tells Sally that the point must lie on the if r is positive orifr is negativeThe radius of 4 tells Sally that the point lies on the fourth circle of the polar plane. The value of ris negative，therefore，the point will lie on theoptions are：positive x-axisnegative x-axispositive y-axisnegative y-axis

Answer 1

A polar coordinate system is expressed as a set of coordinates defined as:

`(\text{ r , }\theta\text{ )}`

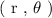
Where,

`\begin{gathered} r\text{ = The magnitude of the radial line} \\ \theta\text{ = Angle of rotation ( anti-clockwise ) measured from +x } \end{gathered}`

Sally tries to plot the following point on a polar coordinate system:

`(\text{ - 4 , }\pi\text{ )}`

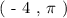
She first tries to determine the line at which the point would lie on. The line of rotation is used to categorize the orientation of the radial line ( r ). So we always first address the coordinate of angle of rotation.

The angle of rotation is:

`\theta\text{ = }\pi`

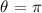
The angle of rotation is always measured from the ( + x-axis ) in the anticlockwise direction. A ( pi or 180 degree ) anticlockwise rotation from the ( + x-axis ) will orient our radial line ( r ) along the ( - x-axis ). As per convention, in this case the radial line magnitude is considered to be positive.

Hence,

`\text{The point must lie on the }\text{\textcolor{#FF7968}{negative x}}\text{ if ( r ) is positive and ( }\theta\text{ = }\pi\text{ )}`

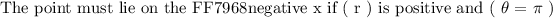
However, if the magnitude of the radial line ( r ) is expressed as a " negative " number. Then the radial line points in the opposite direction than the one as per convention. So the point will lie on the x-axis but due to ( negative ) magnitude of radial line the it must lie on the positive ( x-axis ):

`\text{The point must lie on the }\text{\textcolor{#FF7968}{positive x }}\text{if ( r ) is negative and ( }\theta\text{ = }\pi\text{ )}`

Then we consider the magnitude of the radial vector only which in our case is ( 4 ). So the point must lie on the " fourth unit circle " or a radial distance of 4 units from the origin of polar cooordinate system. Accompained by a negative ( - ) sign it must lie:

`\textcolor{#FF7968}{positive}\text{\textcolor{#FF7968}{ x}}`

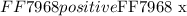
The following in the order of the list of answers:

`\text{\textcolor{#FF7968}{negative x , positive x , positive x}}`