The statement that is true about the function in the graph is A) f(x)=(x-1)^2(x+2). Therefore , A) f(x)=(x-1)^2(x+2) is correct .
let's analyze the statement and the graph further.
The given polynomial is of degree 3, and you claim that the correct expression is f(x)=
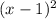 ( x+2).
( x+2).
To verify this, consider the factors in the expression.
If you expand,
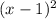 ( x+2) you get a cubic polynomial.
( x+2) you get a cubic polynomial.
Now, examine the behavior of the graph near x-intercepts (points where the graph crosses the x-axis).
For a cubic polynomial, there should be two turning points where the graph changes direction.
The graph exhibits this behavior and the expression matches the given graph, then A) f(x)=(x-1)^2(x+2).
Remember to consider the end behavior of the graph as well, which should reflect the odd degree of the polynomial.
This means that the function has two factors of (x-1) and one factor of (x+2). The other answer choices do not have the correct roots.
This is because the graph has a double root at x=-1 and a single root at x=2.
Question
The graph shows a polynomial function f(x) of degree 3. Which statement about f(x) is true?
A) f(x)=(x-1)^2(x+2)
B) f(x)=(x+1)^2(x-2)
C) f(x)=(x+2)^2(x-1)
D) f(x)=(x-2)^2(x-1)