Question

How will the graph of log x compare to the graph of ln x?

Answer 1

Both graphs pass through (1,0). Both graphs have an asymptote which is the y axis and the graph drops towards -∞ as x goes from 1 to zero. The graph of log x is shallower (assuming base 10) than ln x. For example log 10 = 1 but ln 10 is about 2.3. This value is constant when comparing the y values for the two functions. Log 100 = 2 but ln 100 = 4.6 which is 2.3 times 2. As x increases the graphs of both functions have a shallower gradient.

Answer 2

Answer and Explanation :

To find : How will the graph of
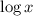`\log x` compare to the graph of
`\ln x`?

Solution :

We know that,

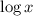`\log x` means the base 10 logarithm.

`\ln x` means the base e logarithm.

The graph of
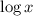`\log x` and
`\ln x` touches at point (1,0).

The graph of
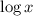`\log x` is stretched more as x increases, the y values continue to increase.

The graph of
`\ln x` increases at a faster rate as x increases.

The major difference between them is to be that the y-values in the natural log graph increase at a faster rate than the y-values for the common logarithm graph.

Refer the attached figure below.