Question

An astronaut has a mass of 82.0 kg. What is the astronaut's stationary weight at a position 4230 kilometers above Earth's surface? Note: Earth's radius is 6380 km.

Answer 1

The stationary weight of the astronaut at a position 4230 kilometers above Earth's surface is approximately 680.5 Newtons.

Step-by-step explanation:

First, we need to calculate the distance, r, from the center of the Earth to the position 4230 kilometers above Earth's surface. The radius of the Earth, R, is given as 6380 km. So, r = R + 4230 km = 6380 km + 4230 km = 10610 km.

Next, we can use Newton's law of universal gravitation to find the gravitational force, F, on the astronaut. The formula is F = (G * m1 * m2) /
`r^2`, where G is the gravitational constant, m1 is the mass of the astronaut, and m2 is the mass of the Earth. Plugging in the values, we get F =
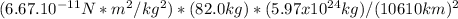`(6.67 . 10^(-11) N*m^2/kg^2) * (82.0 kg) * (5.97 x 10^(24) kg) / (10610 km)^2`. Simplifying this calculation gives approximately 680.5 Newtons.

Answer 2

The acceleration of gravity is inversely proportional to the square of
the distance from the Earth's center. So out where the astronaut is,
the value of gravity will be

(9.81 m/s²) · (4230/6380)² = about 4.31 m/s² .

No matter where she is, her weight is always

(mass) x (gravity in that place)

= (82 kg) x (4.31 m/s²) = 353.6 Newtons