Question

Joe has 20 hot dogs. He is purchasing more hot dogs. He can purchase up to 8 boxes of hot dogs. Each box contains 48 hot dogs. Joe cannot purchase partial boxes. The function that models the number of hot dogs Joe has is f(b)=48b+20f(b)=48b+20 , where b is the number of boxes of hot dogs he purchases.

What is the practical domain of the function?

all real numbers from 1 to 8 inclusive

{68,116,164,212,260,308,356,404}{68,116,164,212,260,308,356,404}

all integers from 1 to 8 inclusive

all real numbers

Answer 1

{68,116,164,212,260,308,356,404}

Both options are the same

Answer 2

All integers from 1 to 8.

Explanation:

We know that:

• Jose has 20 hot dogs.
• He can purchase up to 8 boxes of hot dogs.
• The function that model the number of hot dogs is:
  `f(b)=48b+20`

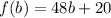
We can observe that the domain of the given function is all values for
`b`, and its range is represented by all the values of
`f(b)`.

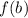So, all practical values that should belong to the domain set is from 1 to 8, only integers numbers, because the problem says that Jose cannot buy incomplete boxes. Therefore, the answer is "all integers from 1 to 8".

It's important to notice that the domain represent the amount of boxes, and the range represent the total number of hot dogs, that's why the domain should be restricted only from 1 to 8, because he can by minimum one box, and maximum 8 boxes.