Question

Determine which of the indicated column vectors are eigenvectors of the given matrix

a. give the corresponding eigenvalue.
a.(6 pts) a = [ 4 2 5 1 ]; ????1 = [ 5 −2 ], ????2 = [ 2 5 ], ????3 = [ −2 5 ]
b.(9 pts) a = [ 1 −2 2 −2 1 −2 2 2

Answer 1

]Eigenvectors are found by the equation
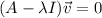
`(A-\lambda I) \vec{v} = 0$` implying that
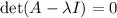
`\det(A-\lambda I) = 0`. We then can write:


`A-\lambda I = \left [ \begin{array}{cc} 4-\lambda & 2 \\ 5 & 1-\lambda \end{array}\right ]`

And:


`\det(A-\lambda I) = (4-\lambda)(1-\lambda) - 10 = 0`

Gives us the characteristic polynomial:


`\lambda^2 - 5 \lambda -6 = 0 \implies \lambda_1 = -1, \lambda_2 = 6`

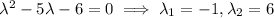
So, solving for each eigenvector subspace:


`\left [ \begin{array}{cc} 4 & 2 \\ 5 & 1 \end{array} \right ] \left [ \begin{array}{c} x \\ y \end{array} \right ] = \left [ \begin{array}{c} -x \\ -y \end{array} \right ]`

Gives us the system of equations:


`4x + 2y = -x \\ewline 5x + y = - y`

Producing the subspace along the line
`y = -(5)/(2) x`

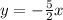
We can see then that 3 is the answer.