Answer:
A)
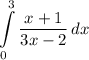
General Formulas and Concepts:
Calculus
Discontinuities
- Removable (Hole)
- Jump
- Infinite (Asymptote)
Integration
- Integrals
- Definite Integrals
- Integration Constant C
- Improper Integrals
Explanation:
Let's define our answer choices:
A)
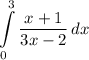
B)

C)
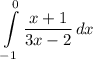
D) None of these
We can see that we would have a infinite discontinuity if x = 2/3, as it would make the denominator 0 and we cannot divide by 0. Therefore, any interval that includes the value 2/3 would have to be rewritten and evaluated as an improper integral.
Of all the answer choices, we can see that A's bounds of integration (interval) includes x = 2/3.
∴ our answer is A.
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration
Book: College Calculus 10e