Question

Dy/dxif y = 4x3 + 3x2 + 2

Answer 1

We can simply solve this mathematical problem by using the following mathematical process.

Here, we will use the general rules for differentiation. Rest of the, procedure are given below -

So,

`= (dy)/(dx)`

`= (d)/(dx) ( {4x}^(3) + {3x}^(2) + 2)`

`= (d)/(dx) ( {4x}^(3)) + (d)/(dx) ( {3x}^(2) ) + (d)/(dx) (2)`

`= (4 * 3 * x {}^((3 - 1)) + (3 * 2 * x {}^((2 - 1)) + 0`

`= 12 {x}^(2) + 6x`

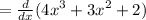
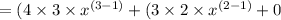
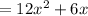
(This will be considered as the final answer of the given differentiation. d/dx of 2 is equal to zero, because 2 is a constant here.)

Hence, the answer will be 12x²+6x

Answer 2

The function is


`\displaystyle{ y=4x^3+3x^2+2`.

We recall that the derivative of each monomial
`ax^b` is
`a\cdot b\cdot x^(b-1)`, and the derivative of a constant (function) is 0.

According to this:


`(d)/(dx)(4x^3+3x^2+2)=4\cdot 3\cdot x^2 + 3\cdot 2\cdot x+0 =12x^2+6x`.


Answer:
`12x^2+6x`