Question

Any number in the form of a+-bi, where a and b are real numbers and b is not equal to 0 is considered a pure imaginary number

Answer 1

wrong those are considered complex numbers. pure imaginary numbers have ,0 for a and are thus in the form. 3i, -2i, 17i. etc

Answer 2

False.

Explanation:

A pure imaginary number is a complex number that doesn't have a real part.

So, if a is a real number, and it doesn't specify that a is only equal to zero, then the expression a+bi is not a pure imaginary number, it's only a complex number. Examples of imaginary numbers are
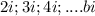`2i;3i;4i;....bi` where
`b\inR`

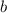
In this case,
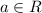`a\in R`, that is, a can be
`0, \±1, \±2, \±3, ...`

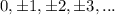
Therefore the statement is false, because a can take any real value.