Answer:

Explanation:
we know that
If a set of ordered pairs represent possible inputs and outputs of the function
then
all ordered pairs of the set must be satisfy the function
we have
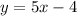
case A)

Point
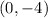
Substitute the value of x and the value of y in the function
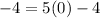
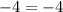 -----> is true
-----> is true
Point
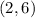
Substitute the value of x and the value of y in the function
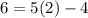
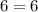 -----> is true
-----> is true
Point
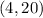
Substitute the value of x and the value of y in the function
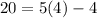
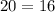 -----> is not true
-----> is not true
therefore
The set case A) not represent possible inputs and outputs of the function
case B)

Point
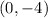
Substitute the value of x and the value of y in the function
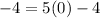
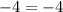 -----> is true
-----> is true
Point
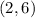
Substitute the value of x and the value of y in the function
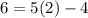
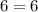 -----> is true
-----> is true
Point
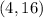
Substitute the value of x and the value of y in the function
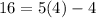
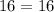 -----> is true
-----> is true
therefore
The set case B) represent possible inputs and outputs of the function
case C) [tex{(0, 4), (2, 6), (4, 16)}[/tex]
Point
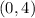
Substitute the value of x and the value of y in the function
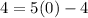
 -----> is not true
-----> is not true
therefore
The set case C) not represent possible inputs and outputs of the function
case D)
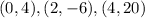
Point
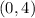
Substitute the value of x and the value of y in the function
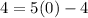
 -----> is not true
-----> is not true
therefore
The set case D) not represent possible inputs and outputs of the function