Answer:
The first positive x-intercept for the function
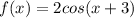 is
is
 .
.
Explanation:
The x-intercept is the point where a line crosses the x-axis,
To find the x-intercept for the function
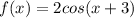 , let's substitute f(x) = 0 into the equation and solve for x:
, let's substitute f(x) = 0 into the equation and solve for x:
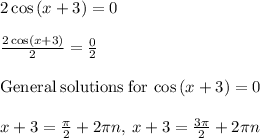
We want the value of the first positive x-intercept so we take the value of
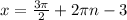 when n = 0.
when n = 0.

We can check our answer with the graph of the function. We can see that we get the same answer.