Given the diagram shows the shape of a putting green in a miniature golf course.
We will find the area of the putting green by dividing it into 3 sections as shown in the following figure:
Area (1) is the area of a rectangle with dimensions 4.5 and 8 feets
so, the area (1) = 4.5 x 8 = 36 feet²
Area (2) is the area of a square with a side length of 4.5 feet
So, the area (2) = 4.5 x 4.5 = 20.25 feet²
Area (3) is the area of the sector of a circle with a radius = 4.5 feet
The sector represents the quarter of the circle
so, Area (3) =
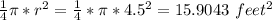
So, the total area is the sum of the three areas:
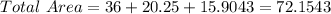
Rounding to the nearest square foot
So, the answer will be: Area = 72 feet²