Question

The diagram shows the shape of a putting green in a miniature golf course. One part of the green is a sector of a circle. To the nearest square foot, what is the area of the putting green?

Answer 1

The area of the putting green is 72.15 ft²

To determine the area, we have that the area of a rectangle is expressed as;

Area = length ×width

Now, substitute the values, we get;

Area = 4.5 ×8

Multiply the values

Area = 36 ft²

For the second rectangle

Area = 4.5 × 4.5

Area = 20.25 ft²

Area of the quarter circle is expressed as;

= πr²/4

Substitute the values

= 3.14 × 4.5²/4

= 3.14 ×20.25/4

Multiply the values and divide, we get;

= 15. 9ft²

Total area = 15.9 + 20.25 + 36

= 72.15 ft²

Answer 2

Given the diagram shows the shape of a putting green in a miniature golf course.

We will find the area of the putting green by dividing it into 3 sections as shown in the following figure:

Area (1) is the area of a rectangle with dimensions 4.5 and 8 feets

so, the area (1) = 4.5 x 8 = 36 feet²

Area (2) is the area of a square with a side length of 4.5 feet

So, the area (2) = 4.5 x 4.5 = 20.25 feet²

Area (3) is the area of the sector of a circle with a radius = 4.5 feet

The sector represents the quarter of the circle

so, Area (3) =

`(1)/(4)\pi *r^2=(1)/(4)*\pi *4.5^2=15.9043\text{ }feet^2`

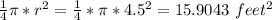
So, the total area is the sum of the three areas:

`Total\text{ }Area=36+20.25+15.9043=72.1543`

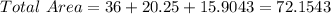
Rounding to the nearest square foot

So, the answer will be: Area = 72 feet²