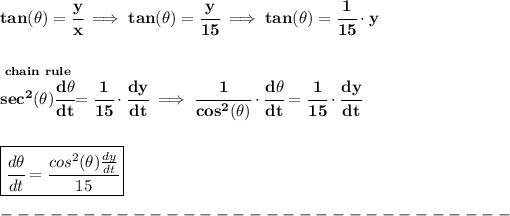Question

Am i correct? calculus

Answer 1

check the picture below.

now, the "x" is a constant, the rocket is going up, so "y" is changing and so is the angle, but "x" is always just 15 feet from the observer. That matters because the derivative of a constant is zero.

now, those are the values when the rocket is 30 feet up above.


`\bf tan(\theta )=\cfrac{y}{x}\implies tan(\theta )=\cfrac{y}{15}\implies tan(\theta )=\cfrac{1}{15}\cdot y \\\\\\ \stackrel{chain~rule}{sec^2(\theta )\cfrac{d\theta }{dt}}=\cfrac{1}{15}\cdot \cfrac{dy}{dt}\implies \cfrac{1}{cos^2(\theta )}\cdot\cfrac{d\theta }{dt}=\cfrac{1}{15}\cdot \cfrac{dy}{dt} \\\\\\ \boxed{\cfrac{d\theta }{dt}=\cfrac{cos^2(\theta )(dy)/(dt)}{15}}\\\\ -------------------------------\\\\`


`\bf cos(\theta )=\cfrac{adjacent}{hypotenuse}\implies cos(\theta )=\cfrac{15}{15√(5)}\implies cos(\theta )=\cfrac{1}{√(5)}\\\\ -------------------------------\\\\ \cfrac{d\theta }{dt}=\cfrac{\left( (1)/(√(5)) \right)^2\cdot 11}{15}\implies \cfrac{d\theta }{dt}=\cfrac{(1)/(5)\cdot 11}{15}\implies \cfrac{d\theta }{dt}=\cfrac{(11)/(5)}{15}\implies \cfrac{d\theta }{dt}=\cfrac{11}{5}\cdot \cfrac{1}{15} \\\\\\ \cfrac{d\theta }{dt}=\cfrac{11}{75}`