Given:
• First choice:
donuts ($0.30/each)
muffins ($0.50/each)
bagels ($0.40/each)
• Second choice (drinks):
Individual cartons of milk or chocolate milk ($0.50/each)
Individual bottles of orange juice or apple juice ($0.75/each)
Given that you must stay within a budget of $100.
Let's solve for the following:
• (1). What food item did you choose? What drink did you choose?
To choose a food item, we must consider that the total cost must not be greater than $100.
Let's choose the following:
Muffins = $0.50 each
Individual cartons of milk or chocolate = $0.50 each
• (2).Write an inequality to represent the cost of the items (less than or equal to $100) in standard form. Use x to represent the number of food items and y to represent the number of drinks.
To write the inequality that represents the cost of the items, we have:
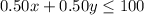
• (3). Solve the inequality for y (slope-intercept form).
Apply the slope-intercept form of a linear equation:
y = mx + b
Where m is the slope.
Rewrite the inequality in part(2) for y.
We have:
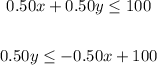
Divide all terms by 0.5:

Therefore, the inequality in slope-intercept form is:
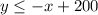
The slope from the inequality is -1.
200 in the inequality means that the total number of items you can buy.
The slope is -1, this means when the number of food item reduces by 1, the number of drinks increase by 1.
• (4). , ,Graph the inequality and describe your graph and the process you used; for example, is your line dotted, solid, or shaded up or down?
Let's graph the inequality using three points.
Let's find values of y using random values of x.
When x = 20:
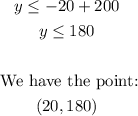
When x = 50:

When x = 100:
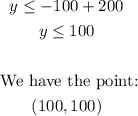
Now, we have the points:
(x, y) ==> (20, 180), (50, 150), (100, 100)
Now, plot the points on a graph and connect the points using a solid line since y is less than or equal to the expression.
Shade the region below the boundary line since y is less than or equal to the expression.
We have the graph below:
• (5). What are the x and y-intercepts?
The x-intercept is the point the line meets the x-axis while the y-intercept is the point it meets the y-axis.
Thus, we have:
x-intercept: (200, 0)
y-intercept: (0, 200)
The x-intercept means the greatest number of food items you can buy is 200
The y-intercept means the greatest number of food items you can buy is 200.
• (6). What are the domain and range in this problem?
The domain is the set of possible x-values.
Thus, we have:
Domain: 0 < x < 200
The range is the set of possible y-values.
Thus, we have:
Range: 0 < y < 200
In this problem, the minimum values of the domain and range is 0 while the maximum is 200. We may not use the minimum and maximum values of the domain and range if it is a must you pick one item each from both categories.
In this case, you have to pick one item from each category, hence we are not required to use the minimum and maximum values.
In a normal linear equation, we can use the minimum value, 0 and the maximum value 200.
The limits for both the domain and range are from 1 to 199.
ANSWER:
1). Muffins = $0.50 each
Individual cartons of milk or chocolate = $0.50 each
2). 0.50x + 0.50y ≤ 100
3). y ≤ -x + 200
4). The graph is attached above.
5). x-intercept: (200, 0)
y-intercept: (0, 200)
(6). Domain: 0 < x < 200
Range: 0 < y < 200