Question

If the number of bacteria in a colony doubles every 210 minutes and the population is currently 8,000 bacteria, what will the population be in 630 minutes and is it modeled by a linear function or a exponential function? A) 24,000; linear function B) 24,000; exponential function C) 64,000; linear function D) 64,000; exponential function

Answer 1

36,00 bacteria

Explanation:

First, find out how many times the population will double. Divide the number of hours by how long it takes for the population to double.

672÷336=2

The population will double 2 times.

Now figure out what the population will be after it doubles 2 times. Multiply the population by 2 a total of 2 times.

9,00022=36,000

That calculation could also be written with exponents:

9,00022=36,000

After 672 hours, the population will be 36,000 bacteria.

Answer 2

Option D. 64000 ; exponential function.

Explanation:

Since number of bacteria in a colony doubles every 210 minutes.

Therefore the function will be modeled by an exponential function with a common ratio of 2.

Currently the population is 8000 bacteria.

Therefore the expression will be

`T_(n)=ar^(nk)`

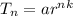
Here a = initial population

n = time or period

Tn = population after n minutes

k = constant

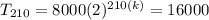
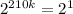
`T_(210)=8000(2)^(210(k))=16000`

`2^(210k)=2^(1)`

210k = 1 ⇒
`k=(1)/(210)`

Now we have to find the population after 630 minutes.

`T_(n)=ar^(nk)`

`T_(630)=8000(2)^{(630)/(210)}=8000(2)^(3)=64000`

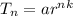
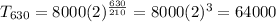
Therefore the answer is option D). 64000 ; exponential function.