Systems of Equations
Given the system:
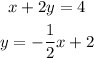
It's required to graph and find the solutions of the system.
Solving the first equation for y:
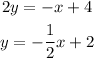
We can see both equations are exactly the same, so there is only one equation and one line.
Let's give x some values and graph the line.
x = 0:
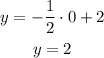
x = 2
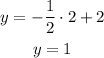
With the points (0, 2) and (2, 1) we graph the line as follows.
Since the number of equations is greater than the number of unknowns, the system has infinitely many solutions. For example, (0, 2) and (2, 1) are solutions for the system.