Question

If you transform y = 2x^2 into y = 10x^2, which option below describes the effect of this transformation on the graph of the quadratic function along the y-axis?

Answer 1

don't know how the multiple choices are worded, but you can match the choices with these words:
it is stretched along the y axis by a factor of 5.
vertically stretched by a factor of 5,
horizontally compressed by a factor of 5

Answer 2

Stretch function:

If a function y =f(x) ;

then a new function g(x) =c f(x) ,where c is constant , is a vertical stretch or vertical compression of the f(x)

• If c > 1, then the graph will be stretched.

• If 0<c<1; then the graph will be compressed

As per the statement:

Given the parent function:
`y =2x^2`

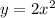
then;

Vertically Stretch the parent function by a factor 5 > 1

then we get a new function;

`y = 5 \cdot (2x^2) = 10x^2`

Therefore, the transformation stretches the graph by a factor of 5.

As you can see the graph of these functions as shown below