Answer:
A.
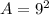
C.
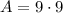
D.
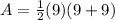
Explanation:
We have been given that a square has side lengths of 9. We are asked to choose the correct options that represent area of the given square.
We know that area of a square is square of its each side.
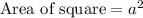 , where a represents each side of the square.
, where a represents each side of the square.
Upon looking at our given choices, we can see that option A is the correct choice as our given square has length of 9 and square of 9 is correct.
We can write area formula as:
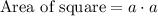
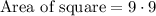
Therefore, option C is correct choice as well.
Upon simplifying option D, we will get:
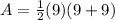
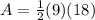
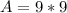
Therefore, option D is correct choice as well.
Upon simplifying option E, we will get:
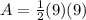

Therefore, option E is not a correct choice.