Question

If the midpoint of a segment is (-6, -16) and one endpoint is (3, 3) What is the other endpoint?

Answer 1

Given a segment defined by the endpoints A(x1,y1) and B(x2,y2), the coordinates of the midpoint from A to B is given by (xm,ym):

`\begin{gathered} x_m=(x_1+x_2)/(2) \\ y_m=(y_1+y_2)/(2) \end{gathered}`

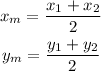
We are given the coordinates of the midpoint (xm,ym)=(-6,-16), and the coordinates of one of the endpoints, say A=(3,3).

We need to find the coordinates of B(x2,y2). Solving the first equation for x2:

`x_2=2x_m-x_1`

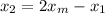
Substituting:

`x_2=2\cdot(-6)-3=-12-3=-15`

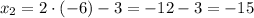
Solving the second equation for y2:

`y_2=2y_m-y_1=2\cdot(-16)-3=-32-3=-35`

Thus, the coordinates of the other endpoint are:

B(-15,-35)