Question

A substance decays so that the amount A of the substance left after t years is given by: A = A 0 · (0.75) t , where A 0 is the original amount of the substance. What is the amount of time it takes for there to be one-third of this substance left, rounded to the nearest tenth of a year?

Answer 1

Let
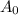
`A_0` be the original amount of the substance. After t years, the amount left A is given by:


`\displaystyle{ A=A_0(0.75)^t`.

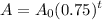
For example, after 1 year, the amount is


`\displaystyle{ A=A_0(0.75)^1=A_0\cdot (0.75)=0.75A_0`.

Thus, after one year, only 0.75=3/4 of the original amount is left.


We want to solve for t, such that
`\displaystyle{ A_0(0.75)^t` is one-third of
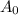
`A_0`, so we set the equation:


`\displaystyle{ \displaystyle{ A_0(0.75)^t= (1)/(3) A_0`.

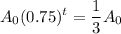
Simplifying by
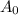
`A_0`, we have:


`\displaystyle{ \displaystyle{(0.75)^t= (1)/(3)`.

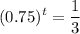
This is an exponential equation, so we can solving it by rewriting it as a logarithm:


`t=\log_(0.75)(1)/(3)\approx 3.8`.


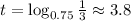
Answer: 3.8