Question

Given the triangle ABC with the points A = ( 4, 6 ) B = ( 2, 8 ) C = ( 5, 10 ) and it's dilation, triangle A'B'C', with points A' = ( 8, 12 ) B' = ( 4, 16 ) C' = ( 10, 20 ) what is the scale factor?

Answer 1

Given the triangle ABC with the points below

`A=(4,6),\text{ }B=(2,8)\text{ and }C=(5,10)`

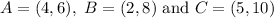
And it's dilation, triangle A'B'C, with points

`A^(\prime)=(8,12),\text{ }B^(\prime)=(4,16)\text{ and }C^(\prime)=(10,20)`

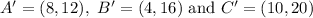
To find the scale factor of dilation, the formula is

Scale factor = Dimension of the new shape ÷ Dimension of the original shape, i.e.

`Scale\text{ factor}=\frac{Dimensio\text{n of the new point}}{Dimension\text{ of the original point}}`

Taking point A and A',

Substituting their dimensions into the scale factor formula

`\begin{gathered} Scale\text{ factor}=((8,12))/((4,6))=(2(4,6))/((4,6))=(2)/(1)=2 \\ Scale\text{ factor}=2 \end{gathered}`

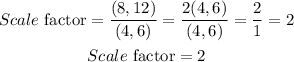
Hence, the scale factor is 2