Question

Find all the zeros of f(x)= x³-14x²+74x-136 given that 5-3i is a zero.

Answer 1

5-3i, 5+3i and 4.

Step-by-step explanation:

Given the function f(x) defined as follows:

`f\mleft(x\mright)=x^3-14x^2+74x-136`

Given that 5-3i is a zero of f(x).

Then, the conjugate of 5-3i must also be a root of f(x).

`\text{Conjugate of 5-3i}=5+3i`

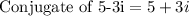
We expand the two roots.

`\begin{gathered} x=5+3i\text{ or x=5-3i} \\ x-(5+3i)=0\text{ or }x-(5-3i)=0 \\ (x-(5+3i))(x-(5-3i))=0 \\ \implies x^2-10x+34=0 \end{gathered}`

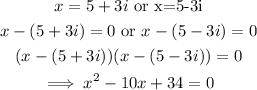
The next step is to divide f(x) by the quadratic polynomial derived above.

`(x^3-14x^2+74x-136)/(x^2-10x+34)=x-4`

Therefore:

`\begin{gathered} x-4=0 \\ x=4 \end{gathered}`

The zeros of f(x) are: 5-3i, 5+3i and 4.