Answer:
5-3i, 5+3i and 4.
Step-by-step explanation:
Given the function f(x) defined as follows:
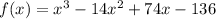
Given that 5-3i is a zero of f(x).
Then, the conjugate of 5-3i must also be a root of f(x).
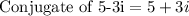
We expand the two roots.
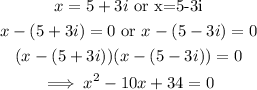
The next step is to divide f(x) by the quadratic polynomial derived above.
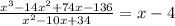
Therefore:
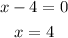
The zeros of f(x) are: 5-3i, 5+3i and 4.