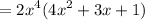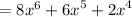Question

Find the product of 2x^4(4x^2 + 3x + 1).

Answer 1

In mathematics, the distributive property is a property that allows us to multiply a mathematical expression by a sum. It states that if A, B, and C are mathematical expressions, then A(B + C) = AB + AC. This property comes in extremely handy in many different problems and applications in mathematics.

`= \displaystyle{ {2x}^(4) (4 {x}^(2) + 3x + 1) }`

`= (2 * 4)x {}^((4 + 2)) + (2 * 3)x {}^(4 + 1) + (2 * 1) {x}^(4)`

`= 8 {x}^(6) + {6x}^(5) + {2x}^(4)`

Answer 2

We want to find the product:


`\displaystyle{ 2x^4\cdot(4x^2 + 3x + 1)`.

By the
`\text{Distributive property}`, we distribute
`2x^4` over each of the three terms inside the parenthesis:


`\displaystyle{ 2x^4\cdot(4x^2 + 3x + 1)=2x^4\cdot4x^2+2x^4\cdot3x+2x^4\cdot1`.

Multiplying the coefficients, and adding the exponents we get:


`8x^6+6x^5+2x^4`.


Answer:
`8x^6+6x^5+2x^4`.