Question

Consider the problem of finding the line of symmetry and vertex of the quadratic equation f(x) =x^2-8x+15 What is the error in the solution below? x^2-8x+15=0 x=-8/2 =-8/2=-4 line of symmetry 8^2-8x+15=0 (-4)^2-8(-4)+15=0 16+32+15=0 y=63 (-4,63) vertex A. The solution is correct. B. The line of symmetry should have been 4 instead of –4. C. The vertex is incorrect; it should have been {–4, 53}. D. -4^2 should have been squared as –16 instead of 16.

Answer 1

We are given the quadratic:


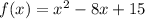
`f(x)=x^2-8x+15`, with a=1, b=-8, c=15.


We know that the x-coordinate of the vertex, which is the point where the line of symmetry passes through is


`\displaystyle{ -(b)/(2a)`.

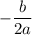
Thus, the x-coordinate of the vertex is
`-(b)/(2a) =-(-8)/(2\cdot1)= (8)/(2)=4`.

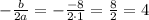
Thus, the line of symmetry is x=4.


Answer: B. The line of symmetry should have been 4 instead of –4.