Question

What are the sine, cosine, and tangent of 5 pi over 4 radians? sin θ = square root 2 over 2; cos θ = negative square root 2 over 2; tan θ = −1 sin θ = negative square root 2 over 2; cos θ = negative square root 2 over 2; tan θ = 1 sin θ = square root 2 over 2; cos θ = negative square root 2 over 2; tan θ = 1 sin θ = negative square root 2 over 2; cos θ = square root 2 over 2; tan θ = −1

Answer 1

Note that we can draw the angle
`\displaystyle{ 5( \pi )/(4)` by adding 5
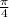
`( \pi)/(4)`'s, as shown in the picture showing the unit circle.

Let the coordinates of
`\displaystyle{ 5( \pi )/(4)` be (-a, -b) , then its reflection in the first quadrant is the angle
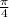
`( \pi)/(4)` (45°) with coordinates (a, b).


We know that
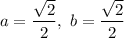
`\displaystyle{ a= ( √(2) )/(2), \ b= ( √(2) )/(2)`, thus the coordinates (-a, -b) which are the cosine and sine of
`\displaystyle{ 5( \pi )/(4)` respectively, are:



`\displaystyle{ a= ( -√(2) )/(2), \ b= ( -√(2) )/(2)`.


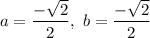
From the identity tan(x)=sin(x)/cos(x), we easily see that the tangent is 1.


Answer:


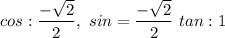
`\displaystyle{ cos:( -√(2) )/(2), \ sin= ( -√(2) )/(2) \ tan: 1`.