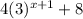Question

PLEASE HELP!!

Let f(x)=2(3)^x+1 +4 .

The graph of f(x) is stretched vertically by a factor of 2 to form the graph of g(x) .

What is the equation of g(x) ?



Enter your answer in the box.

g(x) = ____


I would appreciate if you could also explain the solution and the answer as well ^^

Answer 1

i told u rem is not best girl

f(x) = 2(3)^{x+1} + 4

vertical stretch f(x) by a scale factor of a is a * f(x)

so yeah

g(x) = 2 * f(x)

`g(x) = 2 * (2(3)^(x+1) + 4)`
g(x) = 4(3)^(x+1) + 8 (distributed)

Answer 2

The equation of g(x) is,
`4(3)^(x+1) +8`

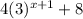
Explanation:

Given the function:
`f(x) = 2(3)^(x+1) + 4`

Vertically stretch states that if y = f(x), then y =a f(x) gives a vertical stretch when a> 1.

It is given that the graph of f(x) is stretched vertically by a factor of 2 to form the graph of g(x)

then by definition of vertical stretch we have;

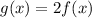`g(x) = 2f(x)` as 2> 1

Then, g(x) becomes =
`2 (2(3)^(x+1) + 4)` =
`4(3)^(x+1) +8`

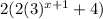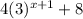
Therefore, the equation of g(x) is,
`4(3)^(x+1) +8`