Question

Use synthetic division to determine whether the number k is an upper or lower bound (as specified for the real zeros of the function f). k = 2; f(x) = 2x3 + 4x2 + 2x - 4; Lower bound?

Answer 1

upper bound

Explanation:

k=2 is not lower bound as seen above

Answer 2

Answer: k = 2 is the upper bond of the given equation.

Explanation:

Here, Given function,

`f(x) = 2x^3 + 4x^2 + 2x - 4`;

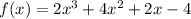Since, the coefficient of
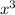`x^3` = 2

The coefficient of
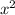`x^2` = 4

The coefficient of
`x` = 2

And, the constant term = - 4

By applying the synthetic division with 2,

The terms in the upper row = 2, 4, 2 and - 4

The terms in the middle row = 4, 16 and 36

And, the terms in the bottom row = 2, 8, 18 and 32

Since, 2> 0 and all the sign in the bottom row are positive.

Thus, 2 is the upper bond for real roots of this equation.