Question

Rewrite the following as a single logarithm. Please show ALL work!

4logx+logy-1/2logz

Answer 1

4 log x = log x^4
1/2 log z = log z^1/2

log x^4 + log y - log z^1/2

= log yx^4 - logz^1/2

= log (y x^4) / z^1/2

Answer 2

Answer:

`\log\left((x^4y)/(√(z))\right)`
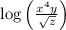
(if this font is too small then try zooming in, or you can check out the attached image which shows the answer in bigger font)

---------------------------------

Work Shown:

I'm going to use the following rules
Rule 1: log(x)+log(y) = log(x*y)
Rule 2: log(x)-log(y) = log(x/y)
Rule 3: y*log(x) = log(x^y)
Rule 4: x^(1/2) = sqrt(x) ... where 'sqrt' stands for 'square root'

Using those rules, we get...
4*log(x)+log(y) - (1/2)*log(z)
log(x^4)+log(y) - log(z^(1/2)) <<-- using rule 3
log(x^4)+log(y) - log(sqrt(z)) <<-- using rule 4
log(x^4*y) - log(sqrt(z)) <<-- using rule 1
log[ (x^4*y)/(sqrt(z)) ] <<-- using rule 2