Question

We have n = 100 many random variables xi 's, where the xi 's are independent and identically distributed bernoulli random variables with p = 0.5 (e(xi)=p and var(xi)=p(1-p)).

a. what distribution does pn i=1 xi follow exactly (sum bernoulli random varaibles)? state the type of distribution and what the parameter is

Answer 1

Recall that for a random variable
`X` following a Bernoulli distribution
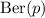
`\mathrm{Ber}(p)`, we have the moment-generating function (MGF)


`M_X(t)=(1-p+pe^t)`

and also recall that the MGF of a sum of i.i.d. random variables is the product of the MGFs of each distribution:


`M_(X_1+\cdots+X_n)(t)=M_(X_1)(t)*\cdots* M_(X_n)(t)`

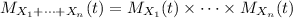
So for a sum of Bernoulli-distributed i.i.d. random variables
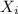
`X_i`, we have


`M_{\sum\limits_(i=1)^nX_i}(t)=\displaystyle\prod_(i=1)^n(1-p+pe^t)=(1-p+pe^t)^n`

which is the MGF of the binomial distribution
`\mathcal B(n,p)`. (Indeed, the Bernoulli distribution is identical to the binomial distribution when
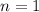
`n=1`.)