We need to graph the following function:
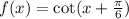
From the expression we can infer the period of the function, which is equal to pi. This is because the cotangent function has the same format at intervals that are equivalent to pi. We also know that there is a phase shift of pi/6 to the left, because the argument of the cotangent has a term "pi/6" being added to "x".
We need to calculate a few points in order to graph this function, a good idea is to calculate the y and x intercepts. This means finding the values at which the graph crosses the axes. This is done by making the whole function equal to 0, then making the value of x equal to 0.
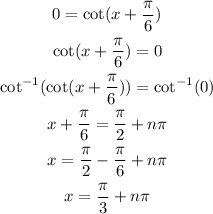
The x-intercepts for the function are the values for the last expression above, where "n" is an integer. This means that the function will cross the x-intercept multiple times. Now we can calculate the y-intercept:
![\begin{gathered} f(0)=\cot (0+(\pi)/(6))_{} \\ f(0)=\sqrt[]{3} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/20a0fn4wi5oqxrc9dq2f.png)
With this we can create the graph of the function, we only need to determine a few x-intercepts. We will use two negative values, and two positive ones.
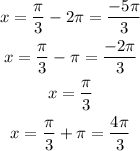
Now we can finally create the graph for the function, which is shown below:
The drawing is not on the correct scale, but it is a representation on how the function should look like.