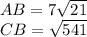Question

Given: ΔABC, CM ⊥ AB AC = 10, CM = 4 AM:BM = 2:5 Find: AB, CB

Answer 1

`AB = 7√(21)\\CB= √(541)`

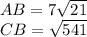
Explanation:

Given: Δ ABC, CM⊥ AB

`AC = 10, CM = 4 AM:BM = 2:5`

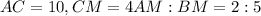
Now, consider
`AM:BM = 2:5 = 2x:5x`

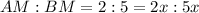
Let In ΔCMA H=- 10 , P= 4 , B= 2x

By, Pythagoras theorem,
`H^2=P^2+B^2`

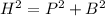
putting values we get,
`10^2=4^2+(2x)^2`

⇒
`100=16+4x^2`

⇒
`x^2= 21`

⇒
`x= √(21)`

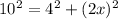
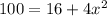
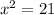
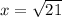
which gives us
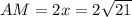`AM = 2x= 2√(21)` and
`MB = 5x= 5√(21)`

⇒
`AB= 2√(21)+5√(21)`

⇒
`AB= 7√(21)`

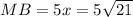
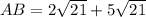
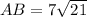
Now, Let In ΔCMB H=- ? , P= 4 , B= 5√21

By, Pythagoras theorem,
`H^2=P^2+B^2`

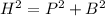
putting values we get,
`H^2=4^2+(5√(21))^2`

⇒
`H^2=16+525`

⇒
`H^2=541`

⇒
`H= √(541)`

⇒
`CB= √(541)`

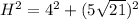
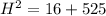
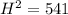
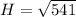
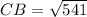
Therefore,
`AB = 7√(21)\\CB= √(541)`