Question

A golf cart travels 70.0 m [E 60° N] in 15.0 s, 100 m east in 20.0 s, and finally 80.0 m [W 45.0° N] in 10.0 s.  Determine the average velocity of the golf cart?

Answer 1

Graphical representation:

Here, OC is the total displacement.

Resolving vector OA into its components.

`OA=70\cos (60\degree)\hat{i}+70\sin (60\degree)\hat{j}\ldots(1)`

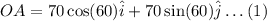
Resolving vector AB into its components.

`AB=100\hat{i}\ldots(2)`

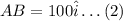
Resolving vector BC into its components.

`BC=-80\cos (45\degree)\hat{i}+80\sin (45\degree)\hat{j}\ldots(3)`

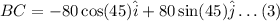
The resultant vector OC is given by the adding equations (1), (2), and (3),

`\begin{gathered} OC=\lbrack70\cos (60\degree)+100-80\cos (45\degree)\rbrack\hat{i}+\lbrack70\sin (60\degree)+80\sin (45\degree)\rbrack\hat{j} \\ =78.43\hat{i}+117.19\hat{j} \end{gathered}`

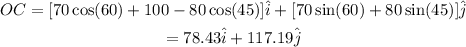
The magnitude of the displacement vector OC is given as,

`\begin{gathered} \lvert OC\rvert=\sqrt[]{(78.43)^2+(117.19)^2} \\ \approx141\text{ m} \end{gathered}`

The average velocity is given as,

`\begin{gathered} v_(av)=\frac{\text{ total displacement}}{\text{total time taken}} \\ =(\lvert OC\rvert)/(t_1+t_2+t_3) \end{gathered}`

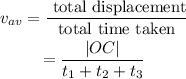
Substituting all known values,

`\begin{gathered} v_(av)=\frac{141\text{ m}}{15\text{ s}+20\text{ s}+10\text{ s}} \\ \approx3.13\text{ m/s} \end{gathered}`

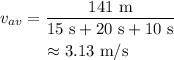
Therefore, the average velocity is 3.13 m/s.