Question

Choose one of the factors of 6x3 + 6.

x − 1
x + 1
x2 − 2x + 1
x2 + x + 1

Answer 1

First thing to do is factor out the common 6 to get
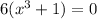
`6(x^3+1)=0`. We have set it equal to 0 so we can solve for the solutions of the polynomial. By the Zero Product Property, either 6 = 0 or
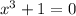
`x^3+1=0`. Of course we know that 6 does not equal 0, so that's not a solution. So
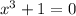
`x^3+1=0`. Solving for x, we have
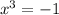
`x^3=-1`. Taking the cubed root of both sides gives us
`x= \sqrt[3]{-1}`. Because the index on our radical is an odd number, 3, we are "allowed" to take the negative of the radicand. The cubed root of -1 is -1, since -1^3 = -1. Therefore, our root is x = -1. Our factor, then is x + 1. Your choice is the second one down. There you go!

Answer 2

The correct option is 2.

Explanation:

The given expression is

`6x^3+6`

Taking gout the common factors.

`6(x^3+1)`

It can be written as

`6(x^3+1^3)`

`6(x+1)(x^2-x+1)`
`[\because a^3+b^3=(a+b)(a^2-ab+b^2)]`

It means 6, (x+1) and
`(x^2-x+1)` is factors of given expression.

Therefore the correct option is 2.