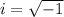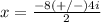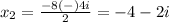Question

Find the discriminant, and determine the number of real solutions. then solve x^2 +8x+20=0

Answer 1

Part 1) The quadratic equation has zero real solutions

Part 2) The solutions are

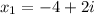`x_1=-4+2i` and
`x_2=-4-2i`

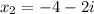
Explanation:

we know that

The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

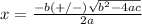
in this problem we have

`x^(2)+8x+20=0`

so

`a=1\\b=8\\c=20`

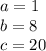
The discriminant is equal to

`D=(b^(2)-4ac)`

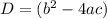
If D=0 -----> the quadratic equation has only one real solution

If D>0 -----> the quadratic equation has two real solutions

If D<0 -----> the quadratic equation has two complex solutions

Find the value of D

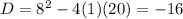`D=8^(2)-4(1)(20)=-16` -----> the quadratic equation has two complex solutions

Find out the solutions

substitute the values of a,b and c in the formula

`x=\frac{-8(+/-)\sqrt{8^(2)-4(1)(20)}} {2(1)}`

`x=\frac{-8(+/-)√(-16)} {2}`

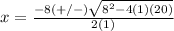
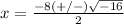
Remember that

`i=√(-1)`

`x=\frac{-8(+/-)4i} {2}`

`x_1=\frac{-8(+)4i} {2}=-4+2i`

`x_2=\frac{-8(-)4i} {2}=-4-2i`