Question

An insurance policy sells for $800. Based on past data, an average of 1 in 50 policyholders will file a $20,000 claim, anaverage of 1 in 250 policyholders will file a$30,000 claim, and an average of 1 in 500 policyholders will file a $60,000 claim. Find the expected value (to the company)per policy sold. If the company sells 30,000 policies, what is the expected profit or loss?The expected value per policy is _____.(Simplify your answer.)

Answer 1

Given data:

1/50 or 0.02 of the policyholders - $20,000 claim

1/250 or 0.004 of the policyholders - $30,000 claim

1/500 or 0.002 of the policy holders - $60,000 claim

Find: expected value per policy sold

Solution:

The formula for expected value is:

`E(x)=\sum ^{}_{}(x_i)p(x_i)`

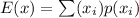
where E(x) = the expected value

xi = the value that x takes

p(xi) = the probability for that x value to occur.

Given the data that we have above, let's plug in those to the formula for expected value.

`\begin{gathered} E(x)=0.02(20,000)+0.004(30,000)+0.002(60,000) \\ E(x)=400+120+120 \\ E(x)=640 \end{gathered}`

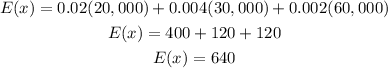
The expected value per policy is $640.